比较两个或更多均值

假设检验是统计分析中最常用的方法之一。Minitab提供了许多假设检验，其中包括 t 检验和方差分析 (ANOVA)。通常，在您进行假设分析时，您假设一种初始声明为真，然后使用样本数据检验该声明。
假设检验包含两个假设（声明）：原假设 (H0) 和备择假设 (H1)。原假设是初始声明，且通常根据先前的研究或常识进行指定。备择假设是可以相信为真实的内容。
假设在前一章中进行的图形分析以及上面的描述性分析，您猜想各出货中心之间的平均交货天数在统计意义上有显著差异。要验证这一点，请执行单因子方差分析，此分析检验两个或更多平均值的等同性。此外，还可执行 Tukey 多重比较检验，以查看哪个出货中心均值存在差异。对于此单因子方差分析，交货天数是响应，出货中心是因子。

执行方差分析

1. 选择统计 > 方差分析 > 单因子。
2. 选择所有因子水平的响应数据位于同一列中。
3. 在响应中，输入天数。在因子中，输入中心。

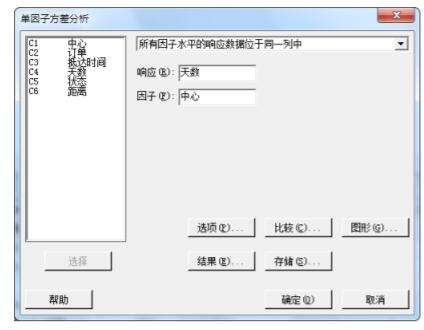
4. 单击比较。

5. 在假设等方差的比较过程下，选中Tukey。

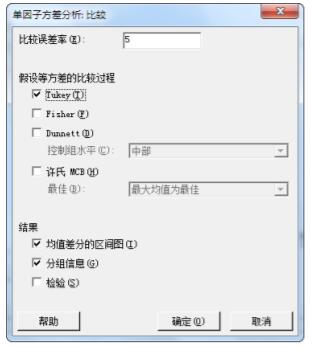
6. 单击确定。
7. 单击图形。
对于许多统计命令，Minitab 都提供了有助于解释结果和评估统计假设有效性的图形。这些图形称为内置图形。
8. 在数据图下，选中区间图、单值图和数据箱线图。
9. 在残差图下面，选择四合一。

10. 单击每个对话框中的确定。

单因子方差分析: 天数 与 中心

方法

原假设 所有均值都相等
备择假设 并非所有的均值都相等
显著性水平 α = 0.05

未使用的行 17
已针对此分析假定了相等方差。

因子信息

因子 水平数 值
中心 3 中部, 东部, 西部

方差分析

来源 自由度 Adj SS Adj MS F 值 P 值
中心 2 114.6 57.317 39.19 0.000
误差 299 437.3 1.462
合计 301 551.9

模型汇总

R-sq（调 R-sq（预
S R-sq 整） 测）
1.20933 20.77% 20.24% 19.17%

均值

中心 N 均值 标准差 95% 置信区间
中部 99 3.984 1.280 (3.745, 4.223)
东部 101 4.452 1.252 (4.215, 4.689)
西部 102 2.981 1.090 (2.746, 3.217)
合并标准差 = 1.20933

Tukey 配对比较

使用 Tukey 方法和 95% 置信度对信息进行分组
中心 N 均值 分组
东部 101 4.452 A
中部 99 3.984 B
西部 102 2.981 C

不共享字母的均值之间具有显著差异。

解释结果

假设检验的决策过程基于 p 值，该值可指示在原假设实际上为真时，错误否定原假设的概率。

• 如果p 值小于或等于预先确定的显著性水平（用 α 或 alpha 表示），则否定原假设，转而支持另一个假设。
• 如果 p 值大于 α 水平，则不能否定原假设，也不能声明支持备择假设。
在 α 等于 ..05 时，方差分析表中的 p 值 (....000) 可提供足够的证据用于判断至少两个出货中心的平均交货时间显著不同。
Tukey 检验的结果包含在分组信息表中，其中列出了显著性和非显著性比。由于每个出货中心在不同的组中，所有出货中心的平均交货时间相互之间也显著不同